递归就是一个函数直接或间接地调用自身。一般来说,递归需要有边界条件、递归前进段、递归返回段。当边界条件不满足时,递归前进;边界条件满足时,递归返回。使用递归时,需要注意以下两点:
下面是使用线性递归实现斐波那契数列的例子(Golang 版):
package main
import "fmt"
func Fibo(n int) int {
if n < 2 {
return 1
}
return Fibo(n-1) + Fibo(n-2)
}
func main() {
// 1 1 2 3 5 8 13
fmt.Println(Fibo(6))
}
为帮助思考和表述递归算法的思路,使算法更直观和清晰,我们定义两个节点:或节点和与节点。
或节点
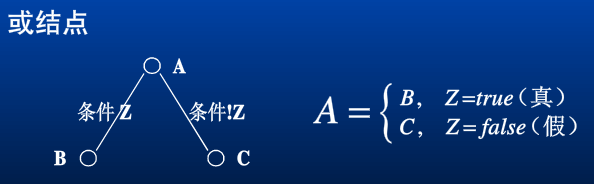
A 为或节点,A 依不同的条件有两种不同的取值,B 或 C。或节点用空心圆表示。
如果多于两种取值,可用如下图表示:
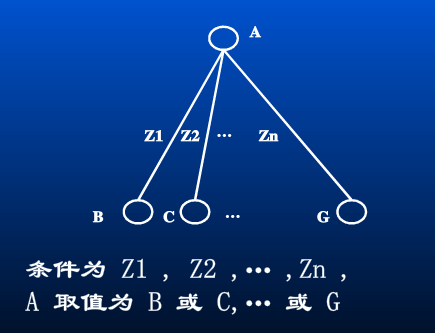
与节点
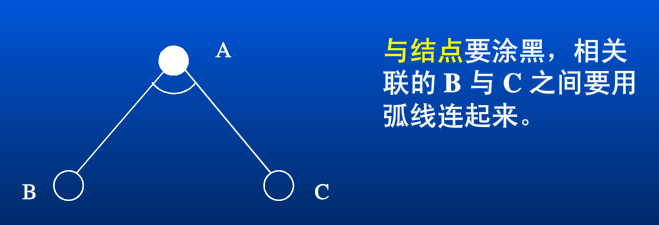
A 为与节点,A 的最终取值是 C 节点的值,但为求得 C 的值,需要先求得 B 节点的值,C 是 B 的函数。
与节点可能有多个相关联的点,这时可描述为下图:
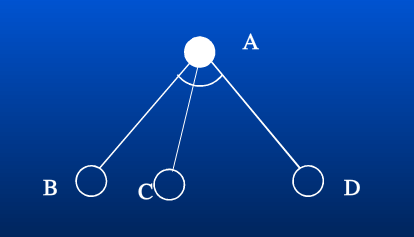
A 的最终取值是 D 节点的值,但是为求得 D 的值,需要先求 B 节点和 C 节点的值。从图上看,需要先求左边的节点的值,才能求最右边的节点的值。我们约定最右边的 D 节点的值就是 A 节点的值。
试编写函数 fact(n),求解 n!。 n! = n * (n-1)!
Golang 线性递归实现:
package main
import "fmt"
func Fact(n int) int {
if n == 1 {
return 1
}
return n * Fact(n-1)
}
func main() {
// 1 * 2 * 3 * 4 * 5 * 6 = 720
fmt.Println(Fact(6))
}
下面是 fact(3) 的调用和返回的递归示意图:
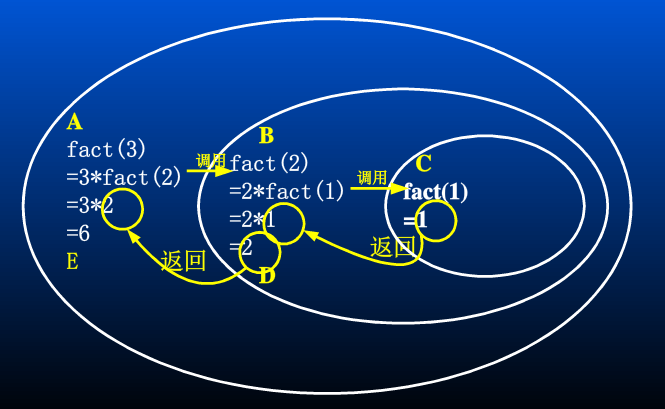
以 n=3 为例,与或节点图如下:
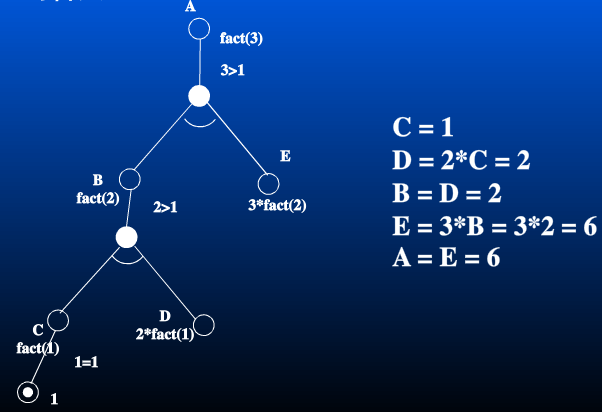
fact(n) 的与或图如下:
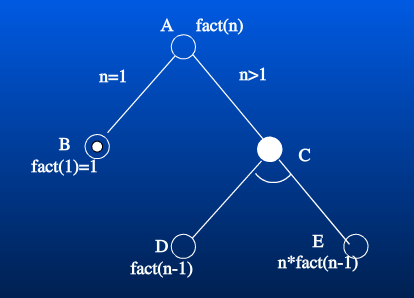
A 为或节点,B 为直接可解节点,值为 1。C 为与节点,当 n > 1 时,A 的值即为 C 的值,而 C 的值即为 E 的值,为求得 E 的值,需要先求出 D 的值,E 是 D 的函数:E = D * n,也就是 E 的值等于 D 的值 fact(n-1) 乘以 n。
递归算法的出发点不在初始条件(递归边界)上,而是在求解目标上,也就是从所求的未知项出发,逐次调用本身,直至递归边界(初始条件)的求解过程。
递归算法比较符合人的思维方式,逻辑性强,可将问题描述的简单扼要,可读性强,易于理解。许多看起来相当复杂、难以下手的问题,如果能够使用递归算法,就会变得易于处理。
快速排序的基本思想:
通过一趟排序将待排序数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
函数 sort 接受两个参数(z 和 y),分别表示数组中一个片段的起始与终止下标值。
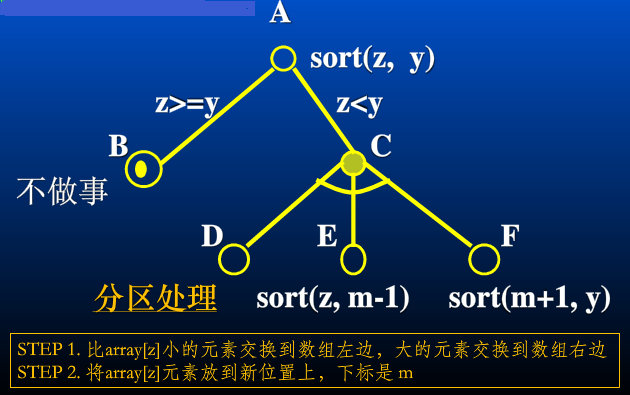
A 是或节点,当 z >= y 时,A 的值是 B 节点的值,B 是直接可解节点(递归边界);当z < y时,A 的值是 C 节点的值,C 节点是与节点,C 节点的值就是 F 节点的值,要想求得 F,需要先求 D、E 的值,F 是 D、E 的函数:分区处理; sort(z, m-1); sort(m+1, y)。
需要特别注意的是分区处理过程。下面是快速排序算法的 Golang 实现:
package main
import (
"cmp"
"fmt"
)
func partition[T cmp.Ordered](arr []T, start, end int) int {
i, j := start, end
pivot := arr[start]
for i < j {
for ; j > i; j-- {
if arr[j] < pivot {
arr[i] = arr[j]
i++
break
}
}
for ; i < j; i++ {
if arr[i] > pivot {
arr[j] = arr[i]
j--
break
}
}
}
arr[i] = pivot
return i
}
func quickSort[T cmp.Ordered](arr []T, start, end int) {
if start >= end {
return
}
m := partition(arr, start, end)
quickSort(arr, start, m-1)
quickSort(arr, m+1, end)
}
func QuickSort[T cmp.Ordered](arr []T) {
quickSort(arr, 0, len(arr)-1)
}
func main() {
arr := []int{0, 111, 2, 1, 1, 5, -1, 6, 4}
QuickSort(arr)
fmt.Println(arr)
}
汉诺塔问题的与或图:
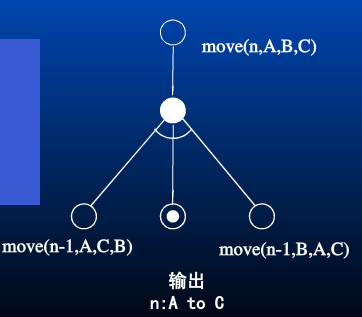
其中 move(n, A, B, C) 的含义是将 n 个盘子从 A 借助 B 搬到 C。
下面是汉诺塔问题的 Golang 实现:
package main
import "fmt"
func Hanoi(n int, A, B, C string) {
if n <= 0 {
return
}
Hanoi(n-1, A, C, B)
fmt.Println(fmt.Sprintf("move #%d from %s to %s.", n, A, C))
Hanoi(n-1, B, A, C)
}
func main() {
Hanoi(4, "A", "B", "C")
}
当递归调用是整个函数体中最后执行的语句,并且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归。
当编译器检测到函数调用是尾递归时,它覆盖当前的活动记录而不是在栈中创建新的。编译器可以做到这点,因为递归调用是当前活跃期内最后一条待执行语句,所以当这个调用返回时帧中没有其他事情可做,因此也就没有保存帧的必要。通过覆盖当前帧而不是在其之上重新添加的方式,这样所使用的栈空间就大大缩减,使得实际的运行效率变得更高。
例子:
Golang 尾递归实现求解 n!:
package main
import "fmt"
func FactTail(n, result int) int {
if n == 1 {
if result == 0 {
return 1
}
return result
}
return FactTail(n-1, result*n)
}
func main() {
fmt.Println(FactTail(6, 1))
}
尾递归极其重要,不用尾递归,函数的栈耗用难以估量,需要保存很多中间函数的栈。比如尾递归 f(n, sum) = f(n-1, sum+value(n)) 只保留后一个函数栈即可,之前的可优化删去。
尾递归从最后开始计算,每递归一次就算出相应的结果,也就是说,函数调用出现在调用者的尾部,因为是尾部,所以根本没有必要保存任何局部变量。直接让被调用的函数在返回时越过调用者,返回到调用者的调用者。
尾递归就是把当前的运算结果(或路径)放在参数里传给下层函数,深层函数所面对的不是越来越简单的问题,而是越来越复杂的问题 —— 因为参数里带有前面若干步的运算路径。对于阶乘而言,越深不意味着越复杂。
尾递归适用于运算对当前递归路径有依赖的问题,传统递归适用于运算对更深层递归有依赖的问题。