循环不变式

循环不变式的主体是不变式，它有三个过程：初始、保持、结束：

• 初始：在循环开始之前，不变式成立
• 保持：在每次循环开始和结束之后，不变式仍然成立
• 结束：循环可以在某些条件下结束。当循环结束时，可以得到期望的结果

综上所述，初始和保持是条件，结束是结论。如果不变式在循环前和每次循环后都成立，那么循环结束时，它仍然成立。

证明Prim算法

Prim 算法的执行过程如下所述：

设 v 为图 g 的顶点集

• 创建只包含起点的顶点集 u、空的边集 e
• 从一端在 u，另一端在 v - u 的所有边中，选择代价最小的，然后将顶点加入到 u 中，边加入到 e 中
• 重复执行上面的步骤，直到 u 等于 v

接下来使用循环不变式证明 Prim 算法：

不变式为：

G 是一个连通网，X 是 G 的顶点集，T 是 G 的最小生成树

初始：

循环开始前，G 中只有一个顶点、T 中只有 0 条边，故不变式成立

保持：

设引入新边 e 之前，子图是 G0，顶点集是 X0，最小生成树是 T0。

引入 e 后，引入的顶点是 y，新的子图是 G1，新的顶点集是 {X0 + y}，新的生成树是 T1。

假设 T1 不是 G1 的最小生成树，那么在 G1 中肯定存在这样的一条边 d：

将 d 加入到 T1，因为 T1 是生成树，所以加入一条边后肯定会形成一个环。设 f 是环上一条代价比 d 大的边，若 f 的一端是 y，那么说明 y 在 e 被引入之前就已经被引入，与引入 e 后，才引入 y 相矛盾，所以 f 的两端一定都在 G0 中。将 f 删掉，可以得到一个代价更小的生成树。

假设 d 的两端都在 G0 中，T0 在去掉 f，加上 d 后，会得到一个代价更小的生成树，这与 T0 是 G0 的最小生成树相矛盾，故 d 一定是：一端在 G0，另一端是 y。

因此，在加入 d 形成的环中，至少包含三条边：d，e，f。且e <= d < f（e 是一端在 G0，另一端是 y 的所有边中代价最小的，所以 e <= d），f 先于 d、e 被引入，f 的两个端点先于 y 被引入（因为 f 已在 G0 中）。

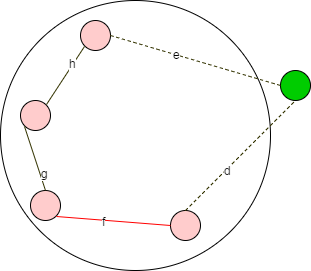
f > d，分为两种情况：

• f 是环上最大的边
  因为 d，e 都比 f 小，所以根据 Prim 算法，d 和（或）e 肯定比 f 先被引入，与 f 先于 e 被引入相矛盾
• 环上有若干条大于等于 f 的边
  道理与【f 是环上最大的边】类似。假设例子中的 h > f，根据 Prim 算法，引入 f 之后会先引入 d，即 d 会先于 h 被引入，与 h 已在 G0 中相矛盾

综上所述，d 是不存在的，因此，T1 是 G1 的最小生成树。

根据循环不变式，在循环结束时，得到的生成树是最小生成树。