最小生成树性质

最小生成树（MST）性质如下所述：

设
  连通网 G = (V, {E})，U 是 V 的非空真子集，(u, v) 是一端在 U，另一端在 V - U 的所有边中代价最小的边
则
  在 G 的所有最小生成树中，一定有一棵包含 (u, v)

证明

下面将使用反证法证明最小生成树性质。

假设 G 的所有最小生成树都不包含 (u, v)，若 T 是 G 的最小生成树，则 T 不包含 (u, v)。在 T 中，一定存在一条边 (u′, v′) 连接 V - U 顶点集和 U 顶点集，该边一端在 U，另一端在 V - U。因为如果不存在这样的边，V - U 和 U 就无法连通，T 就不是生成树。

在下面的最小生成树 T 中，红色的顶点在 V 中，但是不在 U 中，蓝色的点在 U 中：

将 (u, v) 加入到 T：

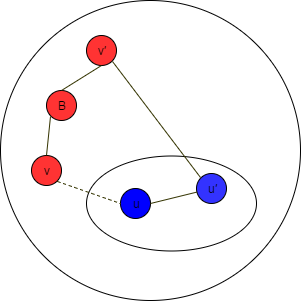
此时会形成一个环：(u, u′, v′, B, v, u)

断开 (u′, v′)，得到新的生成树 T′：

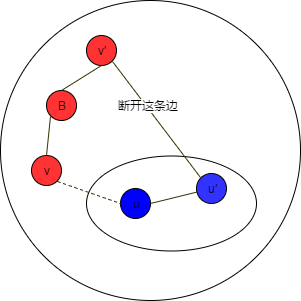
则

cost(T′) = cost(T) + cost(u, v) - cost(u′, v′)

且

cost(u, v) <= cost(u′, v′)

故：

cost(T′) <= cost(T)

因此，T′ 也是 G 的一棵最小生成树，但是它包含 (u, v)，与假设矛盾