Floyd 算法
性质1:
一条最短路径的所有子路径也是最短路径。
从顶点 i 到顶点 j 的最短路径:
- 要么只包含一条直接连接 i 和 j 的弧(或边)
- 要么,经过若干个顶点中转
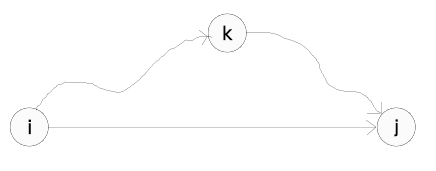
假设 i 到 j 的最短路径需要经过若干个顶点中转,k 是索引值最大的中转顶点,根据性质 1,可以得到:
- (i -> ... -> k) 是 i 到 k 的最短路径,并且这条路径的中间节点都来自 (1 ... k - 1)
- (k -> ... -> j) 是 k 到 j 的最短路径,并且这条路径的中间节点都来自 (1 ... k - 1)
对于任意 k(1 <= k <= n):
当 k = 0 时,意味着无需中转,D[k][i][j] = Weight[i][j]。
否则,存在两种情况:
- 选择 k 作为中继顶点,
D[k][i][j] = D[k-1][i][k] + D[k-1][k][j] - 不选择 k 作为中继顶点,
D[k][i][j] = D[k-1][i][j]
因此 D[k][i][j] = MIN(D[k-1][i][j], D[k-1][i][k] + D[k-1][k][j])。
Floyd 算法本质上是一个动态规划。
可以设置两个辅助数组 D[][] 和 P[][],其中 D[i][j] 用来保存从 i 到 j 的最短路径,初始时,任意两个顶点之间的最短路径是 INFINITY;P[i][j] 用来保存从 i 到 j 所需经过的中继顶点,初始时,P[i][j] = j。对于已经计算出最短路径的两个顶点,可以直接从 D[][] 取值,以防止重复计算,提高执行效率。P[][] 主要用来追踪最短路径。