B+树的性质

一棵 m 阶 B+ 树满足如下性质：

• 每个节点最多有 m 个关键字
• 对于非空树，根节点最少有 1 个关键字
• 除根节点外，其它节点最少有 ceil(m / 2) 个关键字
• 所有叶子节点出现在同一层
• 有 n 个关键字的节点，也有 n 个孩子。其中关键字有序排列，并且对于任意非叶子节点：KeyWord_i 不大于 Children_i 所指向的子树中的所有关键字

在 B+ 树中，所有关键字都存放在叶子节点；而在 B 树中，所有节点都存放关键字。

在 B+ 树中，非叶子节点的关键字，只起索引作用，所以在搜索时，一定要搜索到叶子节点；而在 B 树中，可能无需搜索至叶子节点就可以找到关键字。

在 B+ 树中，所有叶子节点都通过指针连接起来。 B+ 树有两个指针：一个指向根节点；一个指向最左面的叶子节点。

下面的例子是一棵 3 阶 B+ 树：

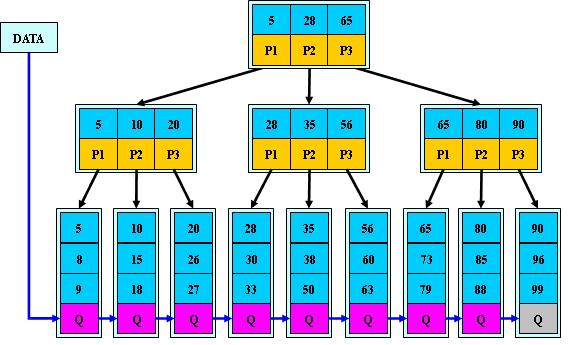
B+树的深度

对于有 n 个关键字的 m 阶 B+ 树而言：

• 当根节点只有 1 个元素，其它节点有 ceil(m / 2) 个元素时，B+ 树的深度最大：
  设 j = ceil(m / 2)、h 为 B+ 树的深度，则：
  2 × (j + j² + ... + j^h-1) + 1 = n ===>
  j × ((1 - j^{h - 1}) / (1 - j)) = (n - 1) / 2 --->
  h = log_j((n + 1) / 2 + (1 - n) / (2 × j) ) + 1
  增长率是 log_mn
• 当每个节点都有 m 个关键字时，树的深度最小：
  设 h 为 B+ 树的深度，则：
  m + m² + ... + m^h = n ===>
  m × ((1 - m^h) / (1 - m)) = n ===>
  h = log_m((m×n-n+m)/m)
  增长率是 log_mn

搜索关键字

从根节点开始

• 首先使用二分查找确定待搜索关键字所在的子树
• 然后逐层向下搜索，直到叶子节点
• 最终如果在叶子节点上搜索到了关键字，则搜索成功，否则搜索失败

插入关键字

从根节点开始

• 首先使用二分查找确定在哪棵子树上插入关键字
• 然后逐层向下搜索，直到叶子节点
• 最终找到插入位置（node，index），其中 node 是叶子节点，index 是插入位置
• 在 node 上插入关键字
• 如果 node 的关键字数量超过最大关键字数量的限制，则从中间位置将 node 一分为二，并将新节点的最小的关键字插入到父节点的关键字列表中；将新节点插入到父节点的孩子节点列表中。然后从父节点开始，继续向上调整，直到节点的关键字数量满足要求，或者回溯到根节点，如果根节点的关键字数量也超过最大关键字数量的限制，那么树将升高一层。

删除关键字

• 首先找到待删除关键字的位置（node，index），其中 node 是叶子节点，index 是待删除关键字在 node 的关键字列表中的索引

• 将关键字从 node 的关键字列表中删除

• 如果 index = 0，那么更新父节点中的索引关键字；如果关键字在父节点的关键字列表中的索引也为 0，那么更新父节点的父节点中的索引关键字；以类似的方式回溯，直到到达根节点，或者关键字在节点的关键字列表的索引不为 0

• 如果 node 是根节点

  • 如果删除关键字后，node 中的关键字数量为 0，那么将树置空，并退出
  • 否则，直接退出，因为 根节点没最小关键字数量的限制

• 如果 node 的关键字数量小于最小关键字数量的限制

  • 如果 node 有左兄弟，并且左兄弟的关键字数量大于最小关键字数量，那么从左兄弟借一个关键字，然后退出
  • 如果 node 有右兄弟，并且右兄弟的关键字数量大于最小关键字数量，那么从右兄弟借一个关键字，然后退出
  • 如果 node 有左兄弟，那么与左兄弟进行合并，合并后父节点的关键字数量将减少 1，因此需要从父节点处继续向上调整，直到到达根节点，或者节点的关键字数量满足要求
  • 如果 node 有右兄弟，那么与右兄弟进行合并，合并后父节点的关键字数量将减少 1，因此需要从父节点处继续向上调整，直到到达根节点，或者节点的关键字数量满足要求
  • 如果 node 既没有左兄弟，也没有右兄弟，说明其父节点只有一个关键字，那么其父节点一定是根节点，此时，将 node 作为新的根节点即可，树的高度将降低 1

Python 实现

tim-chow 的 Github